minisam(三) 例程 gps factor example

2019-10-22 | 阅读：次

说明：本系列博客用来记录本人在学习minisam过程中的理解，方便同大家一起谈论。

1、含有类似gps测量的位姿问题

如图所示，是一个含有类似gps-like factor的二维问题，我们依然使用因子图对其进行求解。

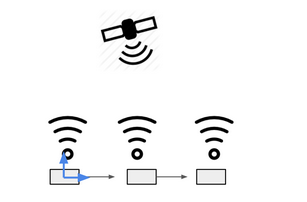
我们定义系统状态变量 $x=\left\{x_{1}, x_{2}, x_{3}\right\}$ ，其中 $x_{i} \in S E(2), i=1,2,3$ 。
本次例程共有二种类型的因子：(1)binary odometry factors;(2)GPS-like factors。用因子图来表示问题模型为：

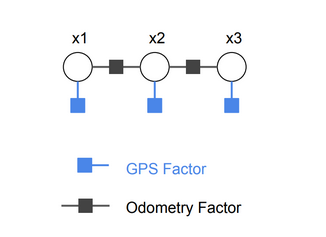
$p(x) \propto \underbrace{p\left(x_{1}, x_{2}\right) p\left(x_{2}, x_{3}\right)}_{\text {odometry }} \underbrace{p\left(x_{1}\right) p\left(x_{2}\right) p\left(x_{3}\right)}_{\text {GPS measurements }}$

如果定义类似gps测量因子是服从高斯分布的，则因子的概率分布为：

$p_{i}\left(x_{i}\right) \propto \exp \left(-\frac{1}{2}\left\|f_{i}\left(x_{i}\right)\right\|_{\Sigma_{i}}^{2}\right)$

其中， $\Sigma_{i}$ 是高斯分布的测量协方差，误差函数 $f_{i}\left(x_{i}\right)$ 为：

$f_{i}\left(x_{i}\right)=\left[\begin{array}{l}{p_{x}-m_{x}} \\ {p_{y}-m_{y}}\end{array}\right]$

误差函数的雅克比矩阵为：

$\frac{\partial f_{i}(x)}{\partial x}=\left[\begin{array}{lll}{1} & {0} & {0} \\ {0} & {1} & {0}\end{array}\right]$

2、c++程序分析

查看所有源程序(含有自己写的中文注释)，点击这里源代码链接

定义gps因子类。

// 定义gps因子类
class GPSPositionFactor : public Factor {
 private:
  Eigen::Vector2d p_;

 public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  GPSPositionFactor(Key key, const Eigen::Vector2d& translation,
                    const std::shared_ptr<LossFunction>& loss)
      : Factor(1, std::vector<Key>{key}, loss), p_(translation) {}
  virtual ~GPSPositionFactor() = default;

  // make a deep copy
  std::shared_ptr<Factor> copy() const override {
    return std::shared_ptr<Factor>(new GPSPositionFactor(*this));
  }

  // 误差 = y - exp(m * x + c);
  Eigen::VectorXd error(const Variables& variables) const override {
    const Sophus::SE2d& pose = variables.at<Sophus::SE2d>(keys()[0]);
    return pose.translation() - p_;
  }

  // 雅克比矩阵
  std::vector<Eigen::MatrixXd> jacobians(
      const Variables& /*values*/) const override {
    Eigen::MatrixXd J(2, 3);
    // clang-format off
        J << 1, 0, 0,
             0, 1, 0;
    // clang-format on
    return std::vector<Eigen::MatrixXd>{J};
  }

  // optional print function
  void print(std::ostream& out = std::cout) const override {
    out << "GPS Factor on SE(2) on " << keyString(keys()[0]) << std::endl;
  }
};

创建因子图框架，加入里程计因子和gps因子。

  // 因子图容器
  FactorGraph graph;

  // 里程计测量的误差函数
  const std::shared_ptr<LossFunction> odomLoss = ScaleLoss::Scale(1.0);

  // 加入里程计因子
  // 在连续位姿之间加入里程计因子
  graph.add(BetweenFactor<Sophus::SE2d>(
      key('x', 1), key('x', 2), Sophus::SE2d(0.0, Eigen::Vector2d(5, 0)),
      odomLoss));
  graph.add(BetweenFactor<Sophus::SE2d>(
      key('x', 2), key('x', 3), Sophus::SE2d(0.0, Eigen::Vector2d(5, 0)),
      odomLoss));

  // gps测量因子误差函数, 二维
  const std::shared_ptr<LossFunction> gpsLoss =
      DiagonalLoss::Sigmas(Eigen::Vector2d(2.0, 2.0));

  // 加入gps因子
  // note that there is no prior factor needed at first pose, since GPS provides
  // the global positions (and rotations given more than 1 GPS measurements)
  graph.add(GPSPositionFactor(key('x', 1), Eigen::Vector2d(0, 0), gpsLoss));
  graph.add(GPSPositionFactor(key('x', 2), Eigen::Vector2d(5, 0), gpsLoss));
  graph.add(GPSPositionFactor(key('x', 3), Eigen::Vector2d(10, 0), gpsLoss));

  graph.print();
  cout << endl;

加入变量初始值和随机噪音

  // 加入变量初始值和随机噪音
  // add random noise from ground truth values
  Variables initials;

  initials.add(key('x', 1), Sophus::SE2d(0.2, Eigen::Vector2d(0.2, -0.3)));
  initials.add(key('x', 2), Sophus::SE2d(-0.1, Eigen::Vector2d(5.1, 0.3)));
  initials.add(key('x', 3), Sophus::SE2d(-0.2, Eigen::Vector2d(9.9, -0.1)));

  initials.print();
  cout << endl;

使用LM优化方法进行优化

  // 使用LM优化方法对初始值进行优化
  LevenbergMarquardtOptimizerParams opt_param;
  opt_param.verbosity_level = NonlinearOptimizerVerbosityLevel::ITERATION;
  LevenbergMarquardtOptimizer opt(opt_param);

  Variables results;

  auto status = opt.optimize(graph, initials, results);
  if (status != NonlinearOptimizationStatus::SUCCESS) {
    cout << "optimization error" << endl;
  }

  results.print();
  cout << endl;

计算边际协方差（误差）

  // 计算所有位姿的边际协方差
  MarginalCovarianceSolver mcov_solver;

  auto cstatus = mcov_solver.initialize(graph, results);
  if (cstatus != MarginalCovarianceSolverStatus::SUCCESS) {
    cout << "maginal covariance error" << endl;
  }

  Eigen::Matrix3d cov1 = mcov_solver.marginalCovariance(key('x', 1));
  Eigen::Matrix3d cov2 = mcov_solver.marginalCovariance(key('x', 2));
  Eigen::Matrix3d cov3 = mcov_solver.marginalCovariance(key('x', 3));

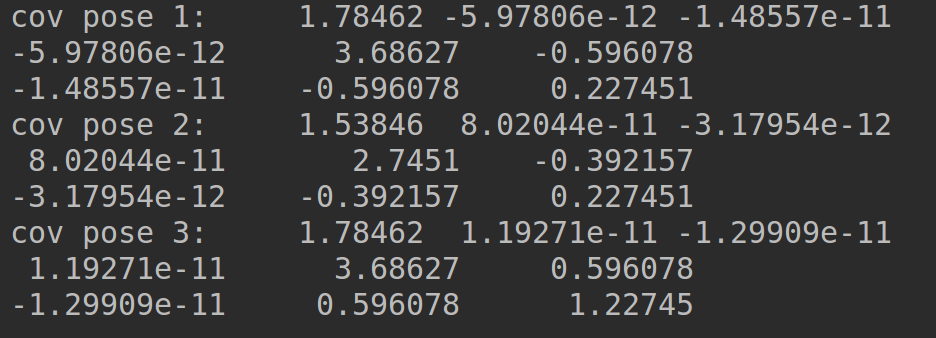
  cout << "cov pose 1:" << cov1 << endl;
  cout << "cov pose 2:" << cov2 << endl;
  cout << "cov pose 3:" << cov3 << endl;

  return 0;

三、代码运行结果分析

显示初始值：

进行优化，显示优化结果：

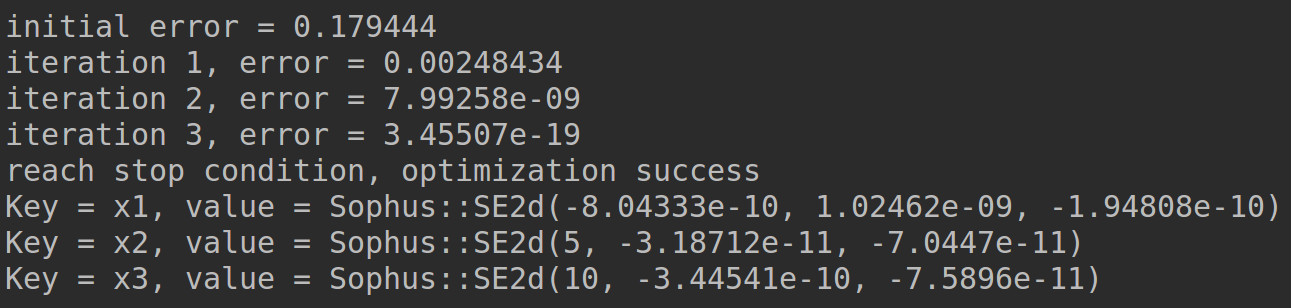
边际协方差：

转载请注明：张鹏辉的博客 » minisam3