说明:本系列博客用来记录本人在学习minisam过程中的理解,方便同大家一起谈论。
一、简单的二维位姿案例
在这里我们使用因子图来解决二维位姿例程。如图所示,
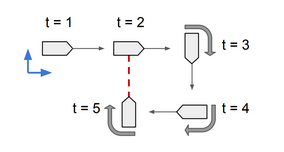
我们要估计小车在时的位姿,定义系统的状态变量:
其中,.
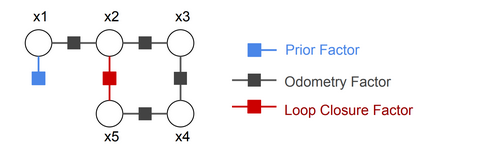
使用因子图将该问题建模为:
二、c++程序分析
查看所有源程序(含有自己写的中文注释),点击这里源代码链接
1.第一步,创建因子图框架,加入一个先验因子(prior factor),中间因子(between factor),各损失函数,闭环约束等。
FactorGraph graph;
// 在第一位置上加入一个先验,并将其设置为原点
// 先验需要在世界坐标系下去修改/校正运行轨迹
// 先验因子包括一个均值和损失函数(协方差矩阵)
const std::shared_ptr<LossFunction> priorLoss =
DiagonalLoss::Sigmas(Eigen::Vector3d(1.0, 1.0, 0.1)); //先验因子的损失函数
graph.add(PriorFactor<Sophus::SE2d>(
key('x', 1), Sophus::SE2d(0, Eigen::Vector2d(0, 0)), priorLoss)); //添加先验因子
// 里程计测量的误差函数
const std::shared_ptr<LossFunction> odomLoss =
DiagonalLoss::Sigmas(Eigen::Vector3d(0.5, 0.5, 0.1));
// 在连续位姿之间添加Between Factor
// 每次前进5个单位,运动到x3-x5时会有向右90°的转动
graph.add(BetweenFactor<Sophus::SE2d>(
key('x', 1), key('x', 2), Sophus::SE2d(0.0, Eigen::Vector2d(5, 0)),
odomLoss));
graph.add(BetweenFactor<Sophus::SE2d>(
key('x', 2), key('x', 3), Sophus::SE2d(-1.57, Eigen::Vector2d(5, 0)),
odomLoss));
graph.add(BetweenFactor<Sophus::SE2d>(
key('x', 3), key('x', 4), Sophus::SE2d(-1.57, Eigen::Vector2d(5, 0)),
odomLoss));
graph.add(BetweenFactor<Sophus::SE2d>(
key('x', 4), key('x', 5), Sophus::SE2d(-1.57, Eigen::Vector2d(5, 0)),
odomLoss));
// 闭环检测的误差函数
const std::shared_ptr<LossFunction> loopLoss =
DiagonalLoss::Sigmas(Eigen::Vector3d(0.5, 0.5, 0.1));
// 加入闭环约束
graph.add(BetweenFactor<Sophus::SE2d>(
key('x', 5), key('x', 2), Sophus::SE2d(-1.57, Eigen::Vector2d(5, 0)),
loopLoss));
graph.print();
cout << endl;
2.第二步,加入变量初始值和随机噪声。
// 加入变量初始值
// 加入随机噪声(自定义?)
Variables initials;
initials.add(key('x', 1), Sophus::SE2d(0.2, Eigen::Vector2d(0.2, -0.3)));
initials.add(key('x', 2), Sophus::SE2d(-0.1, Eigen::Vector2d(5.1, 0.3)));
initials.add(key('x', 3),
Sophus::SE2d(-1.57 - 0.2, Eigen::Vector2d(9.9, -0.1)));
initials.add(key('x', 4),
Sophus::SE2d(-3.14 + 0.1, Eigen::Vector2d(10.2, -5.0)));
initials.add(key('x', 5),
Sophus::SE2d(1.57 - 0.1, Eigen::Vector2d(5.1, -5.1)));
initials.print();
cout << endl;
- 使用Levenberg-Marquard优化方法进行优化,并输出优化结果。
// 调用 LM 方法对初值进行优化
LevenbergMarquardtOptimizerParams opt_param;
opt_param.verbosity_level = NonlinearOptimizerVerbosityLevel::ITERATION;
LevenbergMarquardtOptimizer opt(opt_param);
Variables results;
auto status = opt.optimize(graph, initials, results);
if (status != NonlinearOptimizationStatus::SUCCESS) {
cout << "optimization error" << endl;
}
results.print();
cout << endl;
- 计算边际协方差(误差)
MarginalCovarianceSolver mcov_solver;
auto cstatus = mcov_solver.initialize(graph, results);
if (cstatus != MarginalCovarianceSolverStatus::SUCCESS) {
cout << "maginal covariance error" << endl;
}
Eigen::Matrix3d cov1 = mcov_solver.marginalCovariance(key('x', 1));
Eigen::Matrix3d cov2 = mcov_solver.marginalCovariance(key('x', 2));
Eigen::Matrix3d cov3 = mcov_solver.marginalCovariance(key('x', 3));
Eigen::Matrix3d cov4 = mcov_solver.marginalCovariance(key('x', 4));
Eigen::Matrix3d cov5 = mcov_solver.marginalCovariance(key('x', 5));
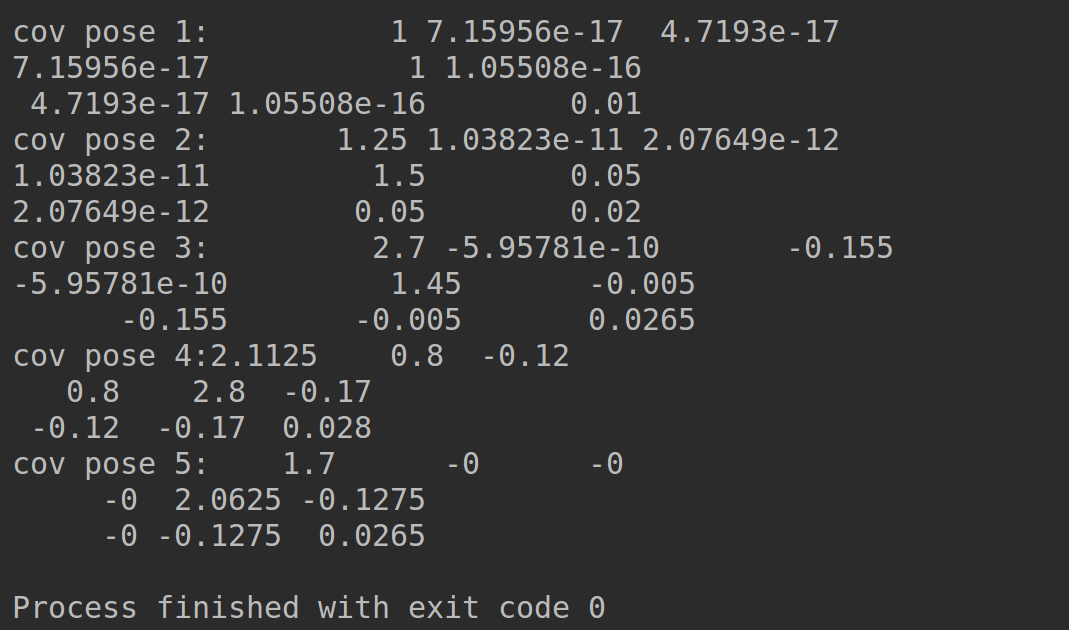
cout << "cov pose 1:" << cov1 << endl;
cout << "cov pose 2:" << cov2 << endl;
cout << "cov pose 3:" << cov3 << endl;
cout << "cov pose 4:" << cov4 << endl;
cout << "cov pose 5:" << cov5 << endl;
三、代码运行结果分析
显示初始值。
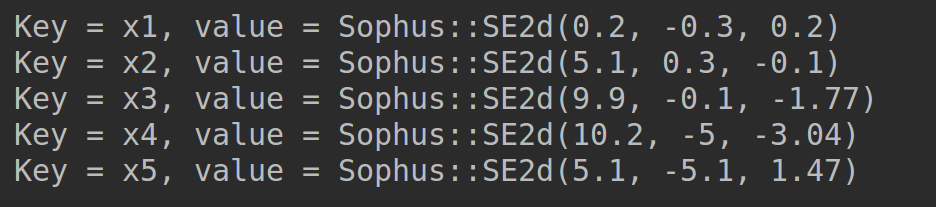
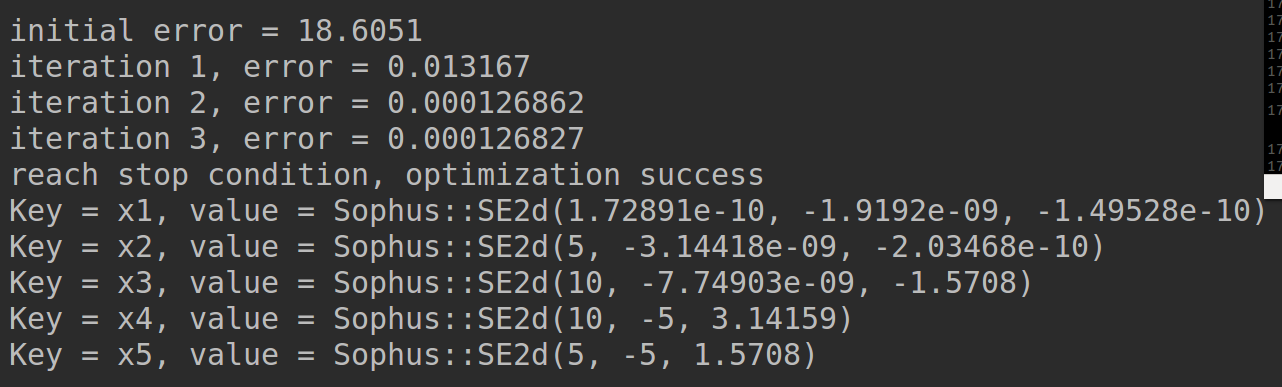
优化结果。如图,起初误差为18.6051,经过三次迭代之后,误差为0.00012…,收敛,优化停止,输出优化后的位姿。
计算的边际协方差结果如图显示,但并不直观,可用matlab工具画图,这里就不予展示了。